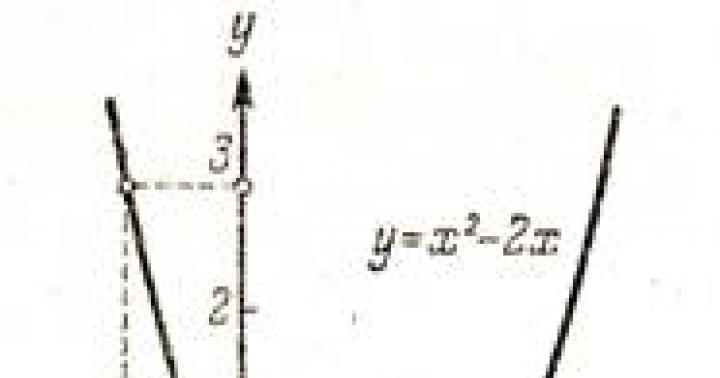Рассматриваются линейные системы нормального вида где а{- - любые числа, а /,(*) - известные функции. В векторной записи неизвестная, а /(*) - известная вектор-функции, А - любая постоянная матрица. Такие системы часто встречаются и в теории дифференциальных уравнений, и в приложениях. Общее решение такой системы в случае f(t) = 0 всегда выражается через элементарные функции. Поэтому такие системы часто применяются для исследования более сложных систем вблизи положения равновесия. В приложениях они появляются, например, при изучении движений в механических системах с несколькими степенями свободы и при описании токов в разветвленных электрических цепях. Путем исключения неизвестных систему можно свести к одному или нескольким уравнениям с одной неизвестной функцией в каждом. Для этого из какого-либо уравнения выражаем одно неизвестное через остальные и подставляем в остальные уравнения системы. Получаем систему с меньшим числом неизвестных. С ней можно поступить аналогично. Этот способ удобен для решения лишь несложных систем. Линейные системы с постоянными коэффициентами I Пример 20. Решить систему Решение примера. Исключаем у. Из первого уравнения имеем у = х" - t. Подставляя во второе уравнение, получаем. Решаем это уравнение методом § 11. Находим. Значит, 1 2. | Решение системы х" = Ах (х 6 Rn) в случае, когда матрица А порядка п имеет п линейно независимых собственных векторов. Так будет в случаях, когда или уравнение det (А-ХЕ) = 0 не имеет кратных корней А, или для каждого кратного корня Л ранг г матрицы А - \Е равен п - к, где к - кратность этого корня (так как уравнение (А - XE)v = 0 для собственных векторов v имеет п - г линейно независимых решений). Пусть А - собственное значение, a v - собственный вектор матрицы А. Тогда х = eMv - частное решение уравнения х1 = Аху так как. Если собственные векторы Vх,..., vn линейно независимы, то имеем решения. Они линейно независимы, так как их вронскиан W Ф 0 при t = 0 (его столбцы vl,..., vn линейно независимы). Следовательно, общее решение системы х* = Ах имеет вид - произвольные постоянные. Лемма 9. Если А{ = а + pi (fi Ф 0) - собственное значение вещественной матрицы A, a vl = (»{,... - собственный вектор для А1# то Aj = Х{ = а - pi - собственное значение, a v2 = v1 = (v},..., - собственный вектор для А2. Для вещественных Хр собственный вектор можно взять вещественным. Доказательство. Имеем Av{ = А^1. Равенство не нарушится, есдй в нем Х{ и координаты вектора v1 заменить сопряженными: Avl = Ajt;1, то есть Для вещественного Хр координаты собственного вектора определяются из системы и вещественными коэффициентами, поэтому вектор v можно взять вещественным Общее решение системы х" = Ах с вещественной матрицей А можно выразить через вещественные функции. Для этого надо взять такие собственные векторы, как в лемме 9, и затем заменить каждую пару комплексных сопряженных решений х1 = eAlV, х2 = eXltv2 парой вещественных решений как в. Получим вещественную фундаментальную систему решений и через нее выразим общее рёшение. I Пример 21. Решить систему Решение примера. Составляем и решаем характеристическое уравнение Линейные системы с постоянными коэффициентами Для находим собственный вектор (^j Можно взять Получаем частное решение Решениями данной системы являются вещественная и мнимая части этого частного решения: J Решение в общем случае. Упростим систему, приведя матрицу А к простейшей форме - жордановой. Известно, что для любой квадратной матрицы А существует такая неособая матрица С, что матрица В = С~[ АС - жорданова, то есть Клетки Ki могут быть любых размеров; в каждой клетке на всей диагонали стоит одно и то же число Af , а в разных клетках А(могут быть различны или одинаковы. Так как Поэтому матрицы С"1 АС и Л имеют одно и то же характеристическое уравнение, значит, одни и те же корни А^ с теми же кратностями. К системе ж" = Ах применяем линейное преобразование координат х = Су у то есть где матрица С та же, что выше. Получаем Умножая слева на С"1, имеем, то есть где матрица Б - жорданова. Если первая клетка имеет размер к х к, вторая - 1x1 и т.д., то в первые к уравнений системы у" = By входят только неизвестные у р..., у*, в следующие I уравнений - только неизвестные yt+1,..., ук+1, и т.д. Значит, система распадается на подсистемы, каждую из которых можно решать отдельно. Первая подсистема имеет вид (где А = Х{) Другие подсистемы отличаются только числами X и к. Сделав в замену, получаем Решая эту систему, начиная с последнего уравнения, находим Умножая на ex,t, получаем решение первой подсистемы Это решение - общее, так как получается из уравнений (73) с помощью тождественных преобразований. Решения других подсистем имеют подобный же вид, лишь числа к = к- и произвольные постоянные cf- будут другими (Лу - число А в j-ft клетке, к - ее размер). Собрав вместе решения всех подсистем, получаем общее решение всей системы у" = By. Возвращаясь от у к ж в силу (72) получаем такой результат. Теорема 16* Общее решение системы х" = Ах есть вектор-функция; у которой каждая координата xi имеет вид где Ар .., Ат - различные собственные значения матрицы А, - алгебраический многочлен, степень которого на 1 меньше размера наибольшей из жордановых клеток, содержащих А;. Коэффициенты многочленов ^(t) (» = 1,..., n; j = 1,..., m) зависят от n произвольных постоянных. Решение конкретной системы х" = Ах можно получить и без приведения матрицы А к жордановой форме. Для этого надо найти все собственные значения Л матрицы А из уравнения det (А - АЕ) - 0. Для каждого А надо найти число т линейно независимых собственных векторов по формуле т = п - г, где п - порядок матрицы А - ХЕ9 г - ее ранг. В случае т = ку где к - кратность корня А, этому корню соответствует решение где Ь!,...,Ь* - линейно независимые собственные векторы. Если матрица А - вещественная, то надо воспользоваться леммой 9 и сказанным после нее. В случае т надо искать решение х = (жр..., хп)Т в виде где 8 = к - пг. Подставляя эти выражения с буквенными коэффициентами а, Ь,... в данную систему, сокращая на е^ и приравнивая коэффициенты при подобных членах, получаем систему линейных алгебраических уравнений для отыскания чисел а, Ь,.... Надо найти общее решение этой системы, зависящее от к произвольных постоянных. (Заметим, что в случае к ^ 4 все старшие коэффициенты в многочленах иногда оказываются равными нулю, но это не мешает найти решение.) Проделав это для каждого А и сложив найденные решения, получим общее решение системы. Если матрица А вещественная, то достаточно проделать описанное только для вещественных корней и для одного из каждой пары комплексных сопряженных корней А = а ± pi {РФ 0), и от полученного решения взять вещественную и мнимую части. Например, из решения х1 = (cj +C2t)elt получаются два решения: u1 = Re хх - (cj + cjt) cos t и u2 = (C3 + cAt) sin t с новыми постоянными Cj,c4. (Обоснование такого метода требует детального анализа и изложено в , § 34.) I Пример 22. Решить систему Решение примера. Составляем и решаем характеристическое урав- нение Для простого корня А = -2 находим собственный вектор (а, р,7) Можно взять а = р = 2, 7 = -2. Имеем частное решение Для кратного корня Л2 3 = 1 находим ранг матрицы А - ХЕ, число m собственньЯТ векторов и степень в многочлена: Ищем решение в виде Подставляем это в данную систему и сокращаем на е*. Приравниваем коэффициенты при подобных членах, начиная со старших: Надо найти общее решение этой системы. Кратность корня Л = 1 равна 2, поэтому все неизвестные а,Ь,... должны выразиться через два из них (пока не знаем, через какие). Из первых трех уравнений имеем Ь = д = 2d. Подставляя в остальные уравнения, получаем Все неизвестные можно выразить через end. Имеем. Полагая d = Cj, с = Cj, получаем. Подставляя это в (77) и прибавляя частное решение (76), умноженное на су получаем общее решение системы: Линейные неоднородные системы с постоянными коэффициентами. Решение такой системы всегда можно получить методом вариации постоянных (п. 5 §9). При этом используется интегрирование. Однако в случае, когда неоднородности f{(t) в системе (70) выражаются только через суммы и произведения функций atm, е7*, cos/3*, sin fit, частное решение системы можно найти без интегрирования - методом неопределенных коэффициентов, как показывается ниже. Так как решение системы х" = Ах + fl(t) +... + fr(t) равно сумме решений систем (xj)" = Axj + fj(t) (j = 1,..., г), а синусы и косинусы по формулам Эйлера выражаются через показательные функции, то достаточно указать вид частного решения системы х" = Ах + рфе7*, где p(t) - amtm + am_xtm~x +... + а0; ао» »ат - векторы. Сделав с этой системой те же преобразования, что в п. 3 с системой х1 = Ах, получаем вместо (74) систему где р*(£) - многочлены степени не выше т. Из этой сибтемы последовательно находим zk, zk_v..., zx. Возможны два случая. Если 7 - А Ф 0, то Jpl(t)eb-»dt = q где ql(t) - многочлен той же степени, что Здесь и далее постоянные интегрирования полагаем равными нулю, так как ищется частное решение. Аналогично отыскиваются zk_v... ,z{. Получаем * где q*(t) - многочлены степени не выше т. Если же 7 - Л = 0, то £ 1, и каждый раз интегрируется только многочлен. От этого его степень повышается на 1. После к интегрирований степень повышается на к. Значит, в этом случае где q*(t) - многочлены степени не выше т + к. Возвращаясь от функций z- к у(и затем к х-, получаем, что система имеет частное решение вида где q^t) - многочлен степени не выше т, если 7 не совпадает ни с одним из корней и степени не выше m + fy, если 7 совпадает с корнем А^.; число к-, равно размеру наибольшей из жордановых клеток, содержащих А;. Следовательно, kj на 1 больше наибольшей степени многочленов, умножаемых на ех"г в общем решении однородной системы. I Пример 23. Решить систему I L Решение примера. Общее решение однородной системы получено в примере 21, здесь А. 2 = 2 ± i. Для неоднородностей 4еи cos* числа 7 = 2и7 = 2 +t различны, поэтому надо решить две системы Для системы (79) 7 = 2^ А;, поэтому частное решение. Подставляя в (79), находим a = Ь = с = 1, d = 0. Значит В системе (80) заменяем 4e2*cos$ на 4е*2+|^. Число 4 рассматриваем как многочлен степени 0. Так как 7 = 2 + i = А, к = 1, то степень многочлена увеличивается на 1 и Подставляя в систему с отброшенным Re получаем Уравнения зависимы, решений много. Берем частное решение, например Общее решение системы х = х0 + х{ + ж2, у = у0 + у! + у2* где ж0, у0 - решение однородной системы (пример 21), а х{, у, х2, у2 найдены здесь. Задачи для упражнений: Линейные системы с постоянными коэффициентами I Системы уравнений, не приведенные к нормальному виду обладают свойствами, отличными от свойств систем вида (70). Согласно , § 11 все решения являются линейными комбинациями решений вида х = r(t)ext, у = s(f)eM, где Л - любой корень характеристического уравнения - многочлены, степень которых меньше кратности к корня А (если Л=1,тоги* - числа), Многочлены могут быть найдены методом неопределенных коэффициентов. Аналогично решаются системы трех и более уравнений. См. задачи в , § 14, б» Известно много способов решения линейных систем с постоянными коэффициентами. Если известны не только числа А, но и базис, в котором матрица А имеет жорданову форму, то решение системы х" = Ах пишется в явном виде (, теорема 11; , § 14, п.З). Операционный метод решения линейных уравнений и систем с постоянными коэффициентами изложен в , §24. Известны условия существования периодического решения системы х1 = Ах 4- f{t) с периодической вектор-функцией f(t) (, гл. 4, §7, п.З).
§2. Задачи на исследование решений линейной системы двух уравнений с двумя неизвестными
Пример 1 . Определить, при каких значениях параметра m система уравнений
имеет единственное решение.
Решение
Система имеет единственное решение, если отношение коэффициентов при х неравно отношению коэффициентов при у:
 .
.
Перейдем от сравнения отношений к сравнению произведений. Тогда в рассмотрение включаются и нулевые значения коэффициентов, зависящих от параметре m .
Решая полученное безразличное неравенство, найдем
3 + 8m + 4m 2 ≠ 4 + 5m ; 4m 2 + 3m – 1 ≠ 0.
Если m 1 и m 2 корни многочлена 4m 2 + 3m – 1 ≠ 0, то
 m
1 = – 1; m
2 = position:absolute;z-index:1;left:0px;margin-left:11px;margin-top:2px; width:14px;height:74px">
m
1 = – 1; m
2 = position:absolute;z-index:1;left:0px;margin-left:11px;margin-top:2px; width:14px;height:74px">
m ≠
или в виде объединения промежутков:
m (– ∞; – 1) (– 1; )(;+∞).
Еще раз отметим, что при m = –EN-US">m = – или при m = –EN-US">m , так же как и при бесчисленном множестве других, удовлетворяющих полученному числовому множеству, данная система будет иметь единственное решение.
Ответ : Система имеет единственное решение, если
m (– ∞; – 1) (– 1; 0,25)EN-US">m и n система уравнений

имеет бесчисленное множество решений.
Решение
Система имеет бесчисленное множество решений, если отношение коэффициентов при х равно отношению коэффициентов при у и равно отношению свободных членов, то есть
Заменим полученную цепочку равенств системой уравнений

Переходя от дробных уравнений к целым. Включаем в рассмотрение и нулевые значения коэффициентов данной системы. (Следует отметить, что не все коэффициенты данной системы могут обращаться в нуль. Один из них EN-US">n ≠ 0. Очевидно, что искомый ответ должен этому условию удовлетворять.)
EN-US">n 2 + n – 6 = 0,
n (n 2 + m ) = 10.
Разрешая относительно и m 1-е и 2-е уравнения системы, получим
n 1 = – 3; n 2 = 2,
m = – n 2.
Откуда
Если n 1 = – 3; Если n 2 = 2,
то m 1 = –– 9 = –; то m 2 = EN-US">m и n в алфавитном порядке, имеем
Ответ: {(–; –3); (1; 2)}
Пример3 . Определить при каких значениях параметра m система уравнений
(2m – 3)x – my = 3m – 2,
(2m + 3)y – 5x + 5 = 0
не имеет решений.
Решение
Система уравнений не имеет решений, если отношение коэффициентов при х равно отношению коэффициентов при у, но неравно отношению свободных членов. Это правило, как и предыдущие, предлагает, что в записи данных уравнений неизвестные находятся в одной (например левой) части равенств и чередуются одинаково. Предполагается так же, что и свободные члены находятся в одной (например правой) части равенств. Удовлетворяя эти требования
(2m – х)x – my = 3m – 2,
– 5x + (2m + 3)у = – 5
и используя признак несовместимости системы, получим
![]()

Система удовлетворяется при m = EN-US">m = 2,25.
Упражнения
1. Определить, при каких значениях параметра m система уравнений
2х + my =5
имеет единственное решение.
Ответ: m (– ∞; – 1,5) position:absolute;z-index:9;left:0px;margin-left:59px;margin-top:23px; width:14px;height:62px"> При каких значениях параметра m система уравнений
(2m + 1)x +7y = 2m ,
Соотношение (в математике) - это взаимосвязь между двумя или более числами одного рода. Соотношения сравнивают абсолютные величины или части целого. Соотношения вычисляются и записываются по-разному, но основные принципы одинаковы для всех соотношений.
Шаги
Часть 1
Определение соотношений-
Определение соотношений. Соотношение - это взаимосвязь между двумя (или более) значениями одного рода. Например, если для приготовления торта необходимы 2 стакана муки и 1 стакан сахара, то соотношение муки к сахару равно 2 к 1.
- Соотношения могут быть использованы и в тех случаях, когда две величины не связаны друг с другом (как в примере с тортом). Например, если в классе учатся 5 девочек и 10 мальчиков, то соотношение девочек к мальчикам равно 5 к 10. Эти величины (число мальчиков и число девочек) не зависят друг от друга, то есть их значения изменятся, если кто-то уйдет из класса или в класс придет новый ученик. Соотношения просто сравнивают значения величин.
-
Обратите внимание на разные способы представления соотношений. Соотношения могут быть представлены словами или при помощи математических символов.
- Очень часто соотношения выражены словами (как показано выше). Особенно такая форма представления соотношений применяется в повседневной жизни, далекой от науки.
- Также соотношения можно выразить через двоеточие. При сравнении двух чисел в соотношении вы будете использовать одно двоеточие (например, 7:13); при сравнении трех и более значений ставьте двоеточие между каждой парой чисел (например, 10:2:23). В нашем примере с классом вы можете выразить соотношение девочек и мальчиков так: 5 девочек: 10 мальчиков. Или так: 5:10.
- Реже соотношения выражаются при помощи наклонной черты. В примере с классом оно может быть записано так: 5/10. Тем не менее это не дробь и читается такое соотношение не как дробь; более того, запомните, что в соотношении цифры не представляют собой часть единого целого.
Часть 2
Использование соотношений-
Упростите соотношение. Соотношение можно упростить (аналогично дробям), разделив каждый член (число) соотношения на . Однако при этом не упустите из виду исходных значений соотношения.
- В нашем примере в классе 5 девочек и 10 мальчиков; соотношение равно 5:10. Наибольший общий делитель членов соотношения равен 5 (так как и 5, и 10 делятся на 5). Разделите каждое число соотношения на 5 и получите соотношение 1 девочка к 2 мальчикам (или 1:2). Однако при упрощении соотношения помните об исходных значениях. В нашем примере в классе не 3 ученика, а 15. Упрощенное соотношение сравнивает количество мальчиков и количество девочек. То есть на каждую девочку приходится 2 мальчика, но в классе не 2 мальчика и 1 девочка.
- Некоторые соотношения не упрощаются. Например, соотношение 3:56 не упрощается, так как у этих чисел нет общих делителей (3 - простое число, а 56 не делится на 3).
-
Используйте умножение или деление для увеличения или уменьшения соотношения. Распространены задачи, в которых необходимо увеличить или уменьшить два значения, пропорциональных друг другу. Если вам дано соотношение и нужно найти соответствующее ему большее или меньшее соотношение, умножьте или разделите исходное соотношение на некоторое данное число.
- Например, пекарю нужно утроить количество ингредиентов, данных в рецепте. Если по рецепту соотношение муки к сахару составляет 2 к 1 (2:1), то пекарь умножит каждый член соотношения на 3 и получит соотношение 6:3 (6 чашек муки к 3 чашкам сахара).
- С другой стороны, если пекарю необходимо уполовинить количество ингредиентов, данных в рецепте, то пекарь разделит каждый член соотношения на 2 и получит соотношение 1:½ (1 чашка муки к 1/2 чашке сахара).
-
Поиск неизвестного значения, когда даны два эквивалентных соотношения. Это задача, в которой необходимо найти неизвестную переменную в одном соотношении при помощи второго соотношения, которое эквивалентно первому. Для решения таких задач пользуйтесь . Запишите каждое соотношение в виде обыкновенной дроби, поставьте между ними знак равенства и перемножьте их члены крест-накрест.
- Например, дана группа учеников, в которой 2 мальчика и 5 девочек. Каково будет число мальчиков, если число девочек увеличить до 20 (пропорция сохраняется)? Во-первых, запишите два соотношения - 2 мальчика:5 девочек и х мальчиков:20 девочек. Теперь запишите эти соотношения в виде дробей: 2/5 и х/20. Перемножьте члены дробей крест-накрест и получите 5x = 40; следовательно, х = 40/5 = 8.
Часть 3
Распространенные ошибки-
Избегайте сложения и вычитания в текстовых задачах на соотношение. Многие текстовые задачи выглядят примерно так: «В рецепте необходимо использовать 4 клубня картофеля и 5 корнеплодов моркови. Если вы хотите добавить 8 клубней картофеля, то сколько понадобится моркови, чтобы соотношение осталось неизменным?» При решении подобных задач ученики часто допускают ошибку, прибавляя одинаковое количество ингредиентов к исходному числу. Однако, чтобы сохранить соотношение, нужно использовать умножение. Вот примеры правильного и неправильного решения:
- Неверно: «8 - 4 = 4 - так мы добавили 4 клубня картофеля. Значит, нужно взять 5 корнеплодов моркови и к ним добавить еще 4... Стоп! Соотношения так не вычисляют. Стоит попробовать снова».
- Верно: «8 ÷ 4 = 2 - значит, мы умножили количество картофеля на 2. Соответственно, 5 корнеплодов моркови тоже нужно умножить на 2. 5 x 2 = 10 - в рецепт нужно добавить 10 корнеплодов моркови». В текстовых задачах гораздо проще распознать ошибку, если записывать единицы измерения после каждого значения. Помните, что величины с одними и теми же единицами измерения в числителе и знаменателе сокращаются. Сократив выражение, вы получите верный ответ.
- Пример: дано 6 коробок, в каждой третьей коробке находится 9 шариков. Сколько всего шариков?
- Неверно: 6 коробок x 3 коробки/9 шариков = ... Стоп, ничего нельзя сократить. Ответ будет таким: «коробки x коробки / шарики». Он не имеет смысла.
- Верно: 6 коробок x 9 шариков/3 коробки = 6 коробок * 3 шарика/1 коробку = 6 коробок * 3 шарика/1 коробку = 6 * 3 шарика/1 = 18 шариков.
Использование соотношений. Соотношения используются как в науке, так и в повседневной жизни для сравнения величин. Простейшие соотношения связывают только два числа, но есть соотношения, сравнивающие три или более значения. В любой ситуации, в которой присутствует более одной величины, можно записать соотношение. Связывая некоторые значения, соотношения могут, например, подсказать, как увеличить количество ингредиентов в рецепте или веществ в химической реакции.
Свободная и вынужденная составляющие переходного процесса и показатели, их характеризующие
2. Два подхода к определению выходного сигнала системы автоматического управления
3. Точность систем автоматического управления и различные способы ее оценки
4. Представление сигнала ошибки замкнутой системы через входной сигнал и его производные. Коэффициенты ошибок
5. Представление выходного сигнала замкнутой системы через входной сигнал и его производные
6. Определение коэффициентов ошибок выходного сигнала через импульсную переходную функцию
7. Соотношение между коэффициентами ошибки замкнутой системы и коэффициентами разложения в ряд Тейлоравыходного сигнала
8. Метод вычисления коэффициентов ошибок через коэффициенты передаточной функции разомкнутой системы
9. Коэффициенты ошибки для систем автоматического управления различного порядка астатизма.
10. Практический способ вычисления коэффициентов ошибок по выражению передаточной функции ошибки
11. Добротность систем автоматического управления
11.1 Сигнал ошибки и коэффициенты добротности для статической системы.
11.2 Сигнал ошибки и коэффициенты добротности для астатической системы первого порядка.
11.3 Сигнал ошибки и коэффициенты добротностидля астатической системы второго порядка.
1. Свободная и вынужденная составляющие переходного процесса и показатели, их характеризующие
При исследовании систем автоматического управления приходится решать задачу обеспечения требуемых показателей качества переходного процесса: быстродействия,колебательности, перерегулирования. Качественные показатели (качество) переходных процессов в системах автоматического управления обычно рассматривается на основе анализа переходных процессов, вызванных внешним воздействием.
Будем полагать, что система автоматического управления описывается линейным дифференциальным уравнением с постоянными коэффициентами.
При изменении внешнего воздействия на входе системы выходную величину можно записать следующим образом: .
где - решение дифференциального уравнения, описывающего систему ;
- свободная составляющая переходного процесса, соответствующая общему решению однородного дифференциального уравнения.
- вынужденная (установившаяся) составляющая переходного процесса, обусловленная законом изменения .
Если дифференциальное уравнениене имеет кратных корней, то свободная составляющая переходного процесса может быть представлена в следующем виде:
где - постоянная интегрирования, значение которой определяют параметры системы и начальные условия;
s, - корни характеристического уравнения замкнутой системы
Качество переходногопроцесса можно оценить по его составляющим и .
В этом смысле различают две группы показателей:
первая- показатели качества переходного процесса ;
вторая - показатели, характеризующие вынужденную (установившуюся) составляющую , по которой определяют точность системы.
Показатели качества, определяемые непосредственно по кривой переходного процесса, называют прямыми оценками качества. Кривая переходного процесса может быть получена теоретически или экспериментально.
В тех случаях, когда расчет переходного процесса связан с большими трудностями, используют косвенные оценки качества. Например, обращаются к косвенным оценкам качества по вещественной частотной характеристике замкнутой системы.
Помимо статистических ошибок, которые будут рассмотрены позже, точность работы систем автоматического управления характеризуетсядинамическимиипереходными ошибками.
Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.
Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.
Линейное уравнение
Уравнения вида ax+by=c называют линейными. Обозначения x, y - это неизвестные, значение которых надо найти, b, a - коэффициенты при переменных, c - свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.
Виды систем линейных уравнений
Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.
F1(x, y) = 0 и F2(x, y) = 0, где F1,2 - функции, а (x, y) - переменные функций.
Решить систему уравнений - это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.
Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.
Если системы имеют одно общее решение или решения не существует их называют равносильными.
Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака "равенство" часть имеет значение или выражена функцией, такая система неоднородна.
Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.
Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.
Простые и сложные методы решения систем уравнений
Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.
Основная задача при обучении способам решения - это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода
Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.
Решение систем методом подстановки
Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе
Приведем решение примера системы линейных уравнений 7 класса методом подстановки:

Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.
Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.
Решение примера системы линейных неоднородных уравнений:

Решение с помощью алгебраического сложения
При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.

Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.
Алгоритм действий решения:
- Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.
- Почленно сложить полученное выражение и найти одно из неизвестных.
- Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.
Способ решения введением новой переменной
Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.
Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.

Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.
Необходимо найти значение дискриминанта по известной формуле: D = b2 - 4*a*c, где D - искомый дискриминант, b, a, c - множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.
Решение для полученных в итоге системы находят методом сложения.
Наглядный метод решения систем
Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.
Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.

Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.
В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.

Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.

Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.
Матрица и ее разновидности
Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. n*m имеет n - строк и m - столбцов.
Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей - вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.
Обратная матрица - это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.
Правила преобразования системы уравнений в матрицу
Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение - одна строка матрицы.
Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.
Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y - только во второй.
При умножении матрицы все элементы матрицы последовательно умножаются на число.
Варианты нахождения обратной матрицы
Формула нахождения обратной матрицы довольно проста: K -1 = 1 / |K|, где K -1 - обратная матрица, а |K| - определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.
Определитель легко вычисляется для матрицы "два на два", необходимо лишь помножить друг на друга элементы по диагонали. Для варианта "три на три" существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.
Решение примеров систем линейных уравнений матричным методом
Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.

В примере a nm - коэффициенты уравнений, матрица - вектор x n - переменные, а b n - свободные члены.


Решение систем методом Гаусса
В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса - Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.
Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 - соответственно с 3-мя и 4-мя переменными.
После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.
В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:

Как видно из примера, на шаге (3) было получено два уравнения 3x 3 -2x 4 =11 и 3x 3 +2x 4 =7. Решение любого из уравнений позволит узнать одну из переменных x n .

Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.
Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.
Для простоты записи вычислений принято делать следующим образом:

Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.
Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака "стрелка" и продолжают выполнять необходимые алгебраические действия до достижения результата.
В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.
Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.
Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.