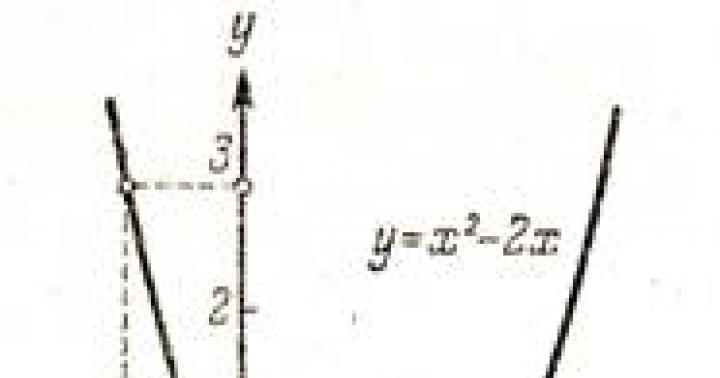Чистая стратегия - детерминированный (исключающий случайности) план действий. В предыдущей главе мы рассматривали только чистые стратегии. Смешанные стратегии будут обсуждаться в параграфе 2.2, а пока, если не оговорено иного, под стратегией мы всегда имеем в виду чистую стратегию.

Очень часто в процессе изложения мы будем иллюстрировать концепции решения примерами биматричных игр, поэтому дадим соответствующие определения.

Определение 2.1. Конечной игрой называется игра, в которой множество игроков и множества стратегий каждого игрока содержат конечное число элементов. Конечная игра двух лиц называется биматричной игрой.

Последнее наименование происходит от удобной формы записи выигрышей в такой игре - с помощью двойной матрицы.

Для последующего анализа удобно разделить стратегии в произвольном профиле стратегий s на стратегию некоторого /-го игрока s, и стратегии всех остальных игроков s_ (. Формально s = (.у, s ,). Здесь не подразумевается, что мы меняем местами координаты профиля стратегий, мы лишь вводим другой способ его обозначения.

Первой концепцией решения игры, которую мы рассмотрим, будет равновесие в доминирующих стратегиях.

Определение 2.2. Стратегия /-го игрока у строго доминирует его стратегию s", если Uj(s jt s ,) > h,(s", s ,) для любого набора s , стратегий остальных игроков. При этом стратегия s" называется строго доминируемой.

Содержательно это означает, что при любом фиксированном наборе стратегий остальных игроков /-Й игрок, выбирая стратегию s, получает строго больший выигрыш, чем при выборе стратегии s". Логично предположить, что рациональный игрок не должен выбирать строго доминируемые стратегии. Такое предположение в простейших играх может оказаться достаточным для нахождения решения игры.

Определение 2.3. Профиль стратегий s* = (s*, s^,..., s*) называется равновесием в (строго) доминирующих стратегиях , если для любого /-го игрока стратегия s" строго доминирует любую другую его стратегию.

Может показаться, что данная концепция решения может привести лишь к тривиальным выводам. Каждый игрок имеет среди своих стратегий такую, которая даст ему выигрыш больше, чем любая другая, как бы ни действовали оппоненты. Тогда он будет применять именно эту стратегию в равновесии. Все довольно очевидно. Но именно такая ситуация характерна для, пожалуй, самой известной и весьма важной для анализа ряда практических ситуаций игры «дилемма заключенных».

Пример 2.1 (дилемма заключенных). Два преступника находятся под стражей в разных камерах и не могут переговариваться. Следствие располагает достаточной доказательной базой, чтобы осудить каждого из них за незначительное преступление на один год. Но по крупному преступлению, за которое преступникам грозит уже десять лет заключения, улик у следствия недостаточно. Представители следствия предлагают каждому из преступников сделку: преступник получит срок на

один год меньше, если он даст свидетельство против своего напарника, которого будет достаточно для обвинения последнего но крупному преступлению. Предположим, что преступников беспокоит только число лет, которое они проведут в тюрьме, каждый дополнительный год дает минус единицу полезности. Тогда выигрыши преступников могут быть представлены следующей двойной матрицей:

В случае, когда участники игры не названы по именам, мы будем считать, что разным стратегиям первого участника соответствуют строки двойной матрицы, а стратегиям второго участника - столбцы. Если в нашем примере первый заключенный даст показания, а второй не будет их давать, то первый будет отпущен на свободу, а второй получит десять лет тюрьмы.

Легко заметить, что, как бы ни действовал другой заключенный, выигрыш больше (срок заключения меньше), если давать показания (для первого игрока первые координаты в первой строке двойной матрицы строго больше, чем во второй строке, для второго игрока вторые координаты в первом столбце двойной матрицы строго больше, чем во втором столбце). Тогда равновесием в доминирующих стратегиях будет профиль стратегий (дать показания, дать показания).

Интересно в данном примере то, что игроки, выбирая поведение, которое увеличивает их выигрыш, приходят к ситуации, где их выигрыши низки по сравнению с противоположной ситуацией - когда оба выбирают молчать. Объяснение кроется в наличии сильного внешнего эффекта, т.е. сильного влияния действий одного игрока на выигрыши другого игрока. В результате равновесный профиль стратегий оказывается единственным неэффективным по Парето в данной игре. Отметим, что эффективность по Парето, желательная с точки зрения участников игры, может быть отнюдь не желательной с общественной точки зрения, как в данном случае.

Ситуации, подобные дилемме заключенных, часто встречаются при анализе экономических ситуаций. Рассмотрим, например, конкуренцию между двумя магазинами, торгующими близким набором продуктов. Для простоты предположим, что магазины могут назначать только два уровня цен - высокий или низкий. Потребители, естественно, предпочитают покупать в магазине с более низкими ценами. Тогда выигрыши магазинов, характеризующиеся их прибылью, могут выглядеть, например, следующим образом:

С точки зрения равновесия ситуация здесь аналогична дилемме заключенных - равновесие в доминирующих стратегиях (низкие цены, низкие цены) является единственным неэффективным по Парето профилем (и тоже желательным с общественной точки зрения).

Уже упомянутая широкая известность дилеммы заключенных стала причиной того, что на ее примере экспериментально пытались проверить корректность предсказаний теории игр. Проверка состояла в том, что двум незнакомым людям предлагалось сыграть в игру на деньги с призами (например, в долларах), близкими к тем, что указаны для игры двух магазинов. Каждый из участников принимал решение отдельно (часто - анонимно) и не знал до получения выигрыша решения другого игрока. Выяснилось, что в таких условиях во многих разыгрываниях игры игроки приходили не к равновесному результату, если предположить, что денежные призы корректно оценивают их выигрыши. Конечно, из результатов этих экспериментов не следует, что предсказания теории игр некорректны, а следует лишь то, что, оценивая свой выигрыш, игроки принимали во внимание неденежные факторы - соображения альтруизма, справедливости и т.п. Если выигрыши игроков оценены корректно, то игроки должны предпочитать доминирующую стратегию, а значит, и выбирать ее (в духе выявленных предпочтений в микроэкономике). Поэтому ценность экспериментов такого рода - не в проверке теоретико-игровых предсказаний, а в оценке роли нематериальной мотивации в действиях индивидов.

Значительно меньше, чем концепция строго доминирования, в теории игр используется концепция слабого доминирования.

Определение 2.4. Стратегия /-го игрока s, слабо доминирует его стратегию s", если m,(s, s ,) > m ; (sJ, s ,) для любого набора стратегий остальных игроков s_j, причем хотя бы для одного набора стратегий других игроков неравенство выполняется строго. Тогда стратегия s" называется слабо доминируемой.

В случае нестрогих неравенств уже нет возможности утверждать, что рациональный игрок не выберет слабо доминируемую стратегию, хотя такое поведение и представляется довольно логичным. Существует, хотя и редко применяется, аналогичное случаю строго доминирования определение равновесия в слабо доминирующих стратегиях.

Определение 2.5. Профиль стратегий s* = (s*, Sj,..., s*) называется равновесием в слабо доминирующих стратегиях , если для любого /-го игрока стратегия s" слабо доминирует любую другую его стратегию.

Пример 2.2 (закрытый аукцион второй цены). Среди двух лиц проводится закрытый аукцион второй цены. Аукцион устроен следующим образом. Каждый из участников указывает неотрицательную ставку, не зная ставок других участников (в конверте). Участник, сделавший наибольшую ставку, выплачивает максимальную сумму среди ставок других участников (т.е. сумму второй но величине ставки) и получает некоторый предмет. Если, например, ставки игроков составили 100 и 90, то побеждает в аукционе участник, сделавший ставку 100, он приобретает предмет за 90 - размер второй ставки. Пусть каждый участник имеет оценку предмета, выраженную в денежных единицах, v 2 > 0. Эти оценки известны всем участникам. Пусть при этом для простоты описания игры если оба участника указывают одинаковую ставку, то предмет достается первому участнику.

В данной игре стратегией первого игрока s, будет размер его ставки. Так как ставка неотрицательна, множество всех его возможных стратегий

5, = выполняется 0 = и,(о, s 2) > w,(s,s 2) = = ц, - s 2 v x слабо доминирует стратегию s,.

Мы показали, что для первого игрока стратегия назвать свою оценку в качестве ставки слабо доминирует любую другую стратегию. Легко проверить, что аналогичное утверждение верно и для второго игрока. Отметим, что в нашем рассуждении мы нигде не использовали тот факт, что игрок знает оценку другого игрока, а значит, и в случае игры с неполной информацией в закрытом аукционе второй цены называть свою оценку будет не менее выгодно, чем делать любую другую ставку.

Может показаться, что для продавца невыгодно устраивать аукцион второй цены, когда он может устроить аукцион первой цены и получать величину не второй, а первой ставки. Однако и величина ставок в случае аукциона первой цены в равновесии будет ниже. Подробнее о доходности аукционов мы поговорим в гл. 5. Пока же отметим, что аукцион второй цены очень поиулярен и широко используется, например, компаниями Google и «Яндекс» при продаже контекстной рекламы в Интернете .

Равновесие в доминирующих стратегиях существует лишь в небольшом классе игр. Обычно у игроков нет единственной стратегии, которая доминирует все прочие. Но концепция доминирования позволяет находить решения в более широком классе игр. Для этого нужно вести последовательные рассуждения о действиях игроков. Мы уже отмечали, что рациональный игрок не будет выбирать строго доминируемую стратегию. Но это означает, что другой игрок может вести анализ игры, игнорируя возможность выбора оппонентом такой стратегии. Возможно, при гаком анализе выяснится, что у другого игрока есть доминируемая стратегия, которая не была доминируемой в исходной игре. И так далее. Дадим формальное определение.

Процесс последовательного исключения строго доминируемых стратегий задается следующим образом. Исключим все строго доминируемые стратегии игроков из рассмотрения, т.е. рассмотрим новую игру, в которой из множества возможных стратегий игроков исключены все доминируемые стратегии. Затем в этой новой игре исключим все строго доминируемые стратегии и т.д.

Возможно, такой процесс завершится, когда у игроков останется по нескольку стратегий, но возможно, что каждый игрок будет иметь лишь одну неисключенную стратегию, тогда логично считать набор из этих стратегий решением игры.

Определение 2.6. Если в результате последовательного исключения строго доминируемых стратегий у каждого игрока остается единственная стратегия, то профиль этих стратегий называется равновесием по доминированию.

В примере 1.1 мы получили именно такое равновесие. Рассмотрим еще один пример.

Профиль стратегий (Н, П) составляет единственное равновесие по Нэшу в данной игре. Но заметим: чтобы выбрать П, второй игрок должен быть уверен, что первый игрок не выберет В. А ведь выигрыш первого игрока одинаков при выборе II вторым игроком. К тому же, выбрав В, первый игрок может не бояться, что второй игрок выберет Л. Возможно, рациональный второй игрок задумается о выборе стратегии Ц.

Второй вопрос, па который пока не найдено какого-то однозначного ответа: как игроки приходят к равновесию по Нэшу?

Идеальный теоретический сценарий здесь такой. Игроки независимо друг от друга формируют ожидания относительно действий других игроков, а затем выбирают действия, которые максимизируют их выигрыш при заданных ожиданиях. Если при этом ожидания соответствуют действиям, реально выбранным игроками, то получаем равновесие по Нэшу. Такая схема рассуждений позволяет назвать равновесие по Нэшу ситуацией с самореализующимися ожиданиями. Но откуда берутся сами ожидания? И какое именно из равновесий по Нэшу, если их несколько, будет выбрано в результате описанного процесса? В рамках рассмотренного сценария эти вопросы остаются без ответа.

Другой подход предполагает наличие обучения игроков. Игроки либо теоретически изучают, как следует играть в данной игре (представьте себе студентов экономического факультета), либо имеют опыт схожего взаимодействия (например, опытный работник приходит в новый коллектив), что позволяет им правильно сформировать ожидания и выбрать оптимальное поведение. Этот сценарий позволяет объяснить формирование ожиданий, но он, во-первых, сокращает область применения игровых моделей только до стандартных, изучаемых и часто встречающихся ситуаций взаимодействия, а во-вторых, может приводить к тому, что не разграничиваются ситуации однократного и повторяющегося взаимодействия, а последние существенно отличаются с точки зрения стратегий и методов решения в рамках теории игр, о чем подробнее будет сказано в гл. 4.

Третий сценарий состоит в том, что существуют предварительная договоренность между игроками, или обычаи, или законы, или указания третьих лиц, которые регламентируют взаимодействие игроков. При этом договоренности или указания могут быть необязательны к исполнению, но если рекомендуется сыграть равновесие по Нэшу, то ни у кого из игроков не возникает желания (в одиночку) отклониться от предписанного поведения. Понятно, что такой сценарий возможен не в любой ситуации. Кроме того, сам процесс формирования договоренности или привлечения третьих лиц может стать частью игры.

Наконец, третий естественный вопрос, который возникает при изучении концепции равновесия по Нэшу, следующий: есть ли эмпирические свидетельства того, что реальные игроки обычно выбирают равновесные стратегии? Здесь снова чрезвычайно сложно дать краткий и однозначный ответ. При этом характер возникающих проблем больше соответствует тематике экспериментальной экономики. Поэтому ограничимся рекомендацией обратиться к специализированной литературе, например, книге , где отлично разобраны вопросы методологии экспериментов и представлен ряд результатов.

Существуют игры, которые не имеют равновесия в чистых стратегиях (см. пример 3.1), поэтому возникает вопрос: какие условия являются достаточными для существования такого равновесия? Сформулируем и докажем утверждение о существовании равновесия по Нэшу в чистых стратегиях в играх, не являющихся конечными.

Утверждение 2.3 . Если множества стратегий каждого из игроков S t являются непустыми выпуклыми компактами в евклидовом пространстве, а функция выигрыша каждого игрока и- непрерывна по s и квазивогнута по 5, то в игре существует равновесие по Нэшу в чистых стратегиях.

Доказательство. Напомним формулировку теоремы Какутаии , которую мы будем использвать при доказательстве. Пусть X - непустое выпуклое компактное множество в R n , X* - множество его подмножеств и/ - такое полунепрерывное сверху отображение из X в X*, что для каждой точки х е X множество f(x) непусто, замкнуто и выпукло. Тогда отображение / имеет неподвижную точку.

Идея доказательства нашего утверждения состоит в построении отображения, удовлетворяющего условиям теоремы Какутани. Для этого несколько переопределим отображение наилучшего ответа. Будем, чисто технически, считать, что наилучший ответ зависит не только от стратегий других игроков, но и от собственной стратегии игрока s y (s). С изменением собственной стратегии игрока при фиксированных стратегиях остальных игроков наилучший ответ, конечно же, меняться не будет. Теперь введем обозначение для отображения наилучшего ответа для всех игроков как декартова произведения s(s ) = s,(s) х s 2 (s) х... х s n (s). Это отображение каждому профилю ставит в соответствие множество профилей, в которых каждый игрок наилучшим образом отвечает на стратегии остальных игроков. Неподвижная точка отображения S, т.е. профиль s такой, что s е s(s)> по определению является равновесием по Нэшу. Покажем, что отображение 5 удовлетворяет условиям теоремы Какутани. Проверка каждого условия будет составлять отдельный пункт доказательства.

• 1. Покажем, что множество S всех профилей - выпуклый компакт. Так как но условию утверждения множества стратегий каждого из игроков S, являются непустыми выпуклыми компактами, то и декартово произведение S = S t X S 2 X ... х S n является выпуклым компактом.
• 2. Отображение s имеет непустые образы. По теореме Вейерштрасса непрерывная функция и- достигает на замкнутом ограниченном множестве 5, своего максимального значения. Следовательно, s имеет непустые образы.
• 3. Образы отображения s замкнуты и выпуклы. Так как функция выигрыша каждого игрока u t квазивогнута по s if то по свойству квазивогнутой функции множество $. = {s. | u t (s i9 s .) > k } при фиксированных s .и k замкнуто при замкнутой области определения и выпукло, если не пусто. Так как это верно для любого k , то верно и то, что множество 5. = {5/1 u t (s", 5 ,) > maxw.(s., s .)}

выпукло. Но тогда и декартово произведение 5(5) = s x (s) х s 2 (S) х... X s n СS) замкнуто и выпукло.

4. Покажем, что отображение § полунепрерывно сверху. Используем условие непрерывности функции и, по s. Доказывать будем от противного. Предположим, что отображение § нс является полунепрерывным сверху. Тогда найдутся последовательности профилей стратегий s m и s m , где т - номер элемента последовательности, такие что для любого т s"" е S, s m е s(s""), lim s"" = s° е S, но lim s"" = s° g lim s(s""). Это означает, что найдется иг-

т~* оо т-> /и -? оо

рок, для которого стратегия s f ° не является наилучшим ответом на s 0 , т.е. найдется стратегия s" такая, что и,(s", s 0 ,) > u,(s] s° ;). Тогда можно найти такое е > 0, чтобы выполнялось m,(s/, s 0 ,) > m,(s ; °, s 0 ,) + Зе, откуда

Поскольку по условию функция м, непрерывна, lim s m = s°, lim s"” = s°,

m * oo m -* oo

при достаточно большом m верно

Объединяя неравенства (2.8)-(2.10) в одну цепочку, получим

Из соотношений (2.11) следует, что u,(s", s"") > m,(s/", s"") + s, но это противоречит условию s"" е s(s""), так как s" дает строго больший выигрыш, чем s/", в ответ на s"". Пришли к противоречию. Следовательно, наша исходная предпосылка, что отображение s не является полунепрерывным сверху, была неверной.

Мы показали, что отображение S удовлетворяет всем условиям теоремы Какутани, а значит, имеет неподвижную точку. Данная неподвижная точка является равновесием по Нэшу. Утверждение 2.3 доказано. ?

Утверждение 2.3, в частности, гарантирует существование равновесия по Нэшу в примере 2.7, но не в примере 2.8, где функции выигрыша игроков разрывны.

" Пример из работы .

Если игра не имеет седловой точки, то возникают затруднения в определении цены игры и оптимальных стратегий игроков. Рассмотрим, например, игру:

В этой игре и . Следовательно, первый игрок может гарантировать себе выигрыш, равный 4, а второй может ограничить свой проигрыш 5. Область между и является как бы ничейной и каждый игрок может попытаться улучшить свой результат за счет этой области. Каковы же должны быть в этом случае оптимальные стратегии игроков?

Если каждый из игроков применяет отмеченную звездочкой стратегию (и ), то выигрыш первого игрока и проигрыш второго будут равны 5. Это невыгодно второму игроку, так как первый выигрывает больше, чем оно может себе гарантировать. Однако если второй игрок каким-либо образом раскроет замысел первого о намерении использовать стратегию , то он может применить стратегию и уменьшить выигрыш первого до 4. Правда, если первый игрок раскроет замысел второго применить стратегию , то, используя стратегию , он увеличит свой выигрыш до 6. Таким образом, возникает ситуация, когда каждый игрок должен хранить в секрете ту стратегию, которую он собирается использовать. Однако, как это сделать? Ведь если партия играется многократно и второй игрок применяет все время стратегию , то первый игрок скоро разгадает замысел второго и, применив стратегию , будет иметь добавочный выигрыш. Очевидно, что второй игрок должен менять стратегию в каждой новой партии, но делать это он должен так, чтобы первый не догадался, какую стратегию применит он в каждом случае.

Для механизма случайного выбора выигрыши и проигрыши игроков будут случайными величинами. Результат игры в этом случае можно оценить средней величиной проигрыша второго игрока. Вернемся к примеру. Так, если второй игрок использует стратегию и случайным образом с вероятностями 0.5; 0.5, то при стратегии первого игрока среднее значение его проигрыша будет:

а при стратегии первого игрока

Следовательно, второй игрок может ограничить свой средний проигрыш значением 4,5 независимо от стратегии, применяемой первым игроком.

Таким образом, в ряде случаев оказывается целесообразным не намечать заранее стратегию, а выбирать ту или иную случайным образом, используя какой-либо механизм случайного выбора. Стратегию, основанную на случайном выборе, называют смешанной стратегией , в отличие от намеченных стратегий, которые называются чистыми стратегиями .

Дадим более строгое определение чистых и смешанных стратегий.

Пусть имеется игра без седловой точки:

Обозначим частоту использования чистой стратегии первого игрока через , (вероятность использования i-ой стратегии). Аналогично обозначим частоту использования чистой стратегии второго игрока через , (вероятность использования j-ой стратегии). Для игры с седловой точкой существует решение в чистых стратегиях . Для игры без седловой точки существует решение в смешанных стратегиях, то есть когда выбор стратегии осуществляется на основании вероятностей. Тогда

Множество чистых стратегий 1-го игрока;

Множество смешанных стратегий 1-го игрока;

Множество чистых стратегий 2-го игрока;

Множество смешанных стратегий 2-го игрока.

Рассмотрим пример: пусть имеется игра

Второй игрок выбирает вероятность . Оценим средний проигрыш второго игрока при применении им стратегий и соответственно.

Выбор игроком того или иного действия называется ходом . Ходы бывают личные (игрок сознательно принимает то или иное решение) и случайные (исход игры не зависит от воли игрока). Набор правил, которые определяют, какой ход игроку необходимо сделать, называется стратегией . Стратегии бывают чистыми (неслучайные решения игроков) и смешанными (стратегию можно рассматривать как случайную величину).

Седловая точка

В теории игр С. т. (седловой элемент ) - это наибольший элемент столбца матрицы игры , который одновременно является наименьшим элементом соответствующей строки (в игре двух лиц с нулевой суммой ). В этой точке, следовательно, максимин одного игрока равен минимаксу другого; С. т. есть точка равновесия .

Теорема о минимаксе

Стратегия, соответствующая минимаксу, называется минимаксной стратегией .

Принцип, диктующий игрокам выбор наиболее "осторожных" максиминной и минимаксной стратегий, называется принципом минимакса . Этот принцип следует из разумного предположения, что каждый игрок стремится достичь цели, противоположной цели противника.

Игрок выбирает свои действия, предполагая, что противник будет действовать неблагоприятным образом, т.е. будет стараться "навредить".

Функция потерь

Функция потерь – функция, которая в теории статистических решений характеризует потери при неправильном принятии решений на основе наблюдаемых данных. Если решается задача оценки параметра сигнала на фоне помех, то функция потерь является мерой расхождения между истинным значением оцениваемого параметра и оценкой параметра

Оптимальная Смешанная стратегия игрока - это полный набор примене­ния его чистых стратегий при многократном повторении игры в одних и тех же условиях с заданными вероятностями.

Смешанная стратегия игрока - это полный набор примене­ния его чистых стратегий при многократном повторении игры в одних и тех же условиях с заданными вероятностями.

1. Если все элементы строки не больше соответствующих элементов другой строки, то исходная строка может быть вычеркнута из платежной матрицы. Аналогично для столбцов.

2. Цена игры единственна.

Док-во: допустим, что есть 2 цены игры v и , которые достигаются на паре и соответственно, тогда

3. Если ко всем элементам платежной матрицы прибавить одно и то же число, то оптимальные смешанные стратегии не изменятся, а цена игры увеличится на это число.

Док-во:
, где

4. Если все элементы платежной матрицы умножить на одно и то же число не равное нулю, цена игры умножится на это число, а оптимальные стратегии не изменятся.

5. ТЕОРИЯ ИГР И СТАТИСТИЧЕСКИХ РЕШЕНИЙ

5.1. Матричная игра с нулевой суммой

Экономико-математическое моделирование осуществляется в условиях:

Определенности;

Неопределенности.

Моделирование в условиях определенности предполагает наличие всех необходимых для этого исходных нормативных данных (матричное моделирование, сетевое планирование и управление).

Моделирование в условиях риска проводится при стохастической неопределенности, когда значения некоторых исходных данных случайны и известны законы распределения вероятностей этих случайных величин (регрессионный анализ, теория массового обслуживания).

Моделирование в условиях неопределенности соответствует полному отсутствию некоторых необходимых для этого данных (теория игр).

Математические модели принятия оптимальных решений в конфликтных ситуациях строятся в условиях неопределенности.

В теории игр оперируют следующими основными понятиями:

Стратегия;

Функция выигрыша.

Ходом будем называть выбор и осуществление игроком одного из предусмотренных правилами игры действий.

Стратегия - это технология выбора варианта действий при каждом ходе в зависимости от сложившейся ситуации.

Функция выигрыша служит для определения величины платежа проигравшего игрока выигравшему.

В матричной игре функция выигрыша представляется в виде платежной матрицы :

где - величина платежа игроку I, выбравшему ход , от игрока II, выбравшего ход .

В такой парной игре значения функций выигрыша обоих игроков в каждой ситуации равны по величине и противоположны по знаку, т. е. и такую игру называют с нулевой суммой .

Процесс "игры в матричную игру" представляется следующим образом:

Задается платежная матрица ;

Игрок I независимо от игрока II выбирает одну из строк этой матрицы, например, -ую;

Игрок II независимо от игрока I выбирает один из столбцов этой матрицы, например, - ый;

Элемент матрицы определяет, сколько получит игрок I от игрока II. Разумеется, если , то речь идет о фактическом проигрыше игрока I.

Антагонистическую парную игру с платежной матрицей будем называть игрой .

Пример

Рассмотрим игру .

Задана платежная матрица:

.

Пусть игрок I независимо от игрока II выбирает 3-ю строку этой матрицы, а игрок II независимо от игрока I выбирает 2-ой столбец этой матрицы:

Тогда игрок I получит 9 единиц от игрока II.

5.2. Оптимальная чистая стратегия в матричной игре

Оптимальной стратегией называется такая стратегия игрока I, при которой он не уменьшит своего выигрыша при любом выборе стратегии игроком II, и такая стратегия игрока II, при которой он не увеличит своего проигрыша при любом выборе стратегии игроком I.

Выбирая в качестве хода -ую строку платежной матрицы, игрок I обеспечивает себе выигрыш не менее величины в наихудшем случае, когда игрок II будет стараться минимизировать эту величину. Поэтому игрок I выберет такую -ую строку, которая обеспечит ему максимальный выигрыш:

.

Игрок II рассуждает аналогично и может наверняка обеспечить себе минимальный проигрыш:

.

Всегда справедливо неравенство:

Величину называют нижней ценой игры .

Величину называют верхней ценой игры .

Оптимальные стратегии и называются чистыми , если для них выполняются равенства:

,

.

Величину называют чистой ценой игры , если .

Оптимальные чистые стратегии и образуют седловую точку платежной матрицы .

Для седловой точки выполняются условия:

т. е. элемент является наименьшим в строке и наибольшим в столбце.

Таким образом, если платежная матрица имеет седловую точку , то можно найти оптимальные чистые стратегии игроков.

Чистая стратегия игрока I может быть представлена упорядоченным набором чисел (вектором), в котором все числа равны нулю, кроме числа, стоящего на - ом месте, которое равно единице.

Чистая стратегия игрока II может быть представлена упорядоченным набором чисел (вектором), в котором все числа равны нулю, кроме числа, стоящего на - ом месте, которое равно единице.

Пример

.

Выбирая в качестве хода какую-нибудь строку платежной матрицы, игрок I обеспечивает себе выигрыш в наихудшем случае не менее величины в столбце, обозначенном :

Поэтому игрок I выберет 2-ую строку платежной матрицы, обеспечивающую ему максимальный выигрыш независимо от хода игрока II, который будет стараться минимизировать эту величину:

Игрок II рассуждает аналогично и выберет в качестве хода 1-ый столбец:

Таким образом, имеется седловая точка платежной матрицы:

соответствующая оптимальной чистой стратегии для игрока I и для игрока II, при которой игрок I не уменьшит своего выигрыша при любом изменении стратегии игроком II и игрок II не увеличит своего проигрыша при любом изменении стратегии игроком I.

5.3. Оптимальная смешанная стратегия в матричной игре

Если платежная матрица не имеет седловой точки, то любому игроку нерационально использовать одну чистую стратегию. Выгоднее использовать "вероятностные смеси" чистых стратегий. Тогда в качестве оптимальных определяются уже смешанные стратегии.

Смешанная стратегия игрока характеризуется распределением вероятности случайного события, заключающегося в выборе этим игроком хода.

Смешанной стратегией игрока I называют такой упорядоченный набор чисел (вектор), который удовлетворяет двум условиям:

1) для , т. е. вероятность выбора каждой строки платежной матрицы неотрицательна;

2) , т. е. выбор каждой из строк платежной матрицы в совокупности представляет полную группу событий.

Смешенной стратегией игрока II будет упорядоченный набор чисел (вектор), удовлетворяющий условиям:

Величина платежа игроку I, выбравшему смешанную стратегию

от игрока II, выбравшему смешанную стратегию

,

представляет собой среднюю величину

.

Оптимальными называют смешанные стратегии

и ,

если для любых произвольных смешанных стратегий и выполняется условие:

т. е. при оптимальной смешанной стратегии выигрыш игрока I наибольший, а проигрыш игрока II наименьший.

Если в платежной матрице нет седловой точки, то

,

т. е. существует положительная разность (нераспределенная разность )

- ³ 0,

и игрокам нужно искать дополнительные возможности для уверенного получения в свою пользу большей доли этой разности.

Пример

Рассмотрим игру , заданную платежной матрицей:

.

Определим, есть ли седловая точка:

, .

Оказывается, что в платежной матрице нет седловой точки и нераспределенная разность равна :

.

5.4. Отыскание оптимальных смешанных стратегий

для игр 2×2

Определение оптимальных смешанных стратегий для платежной матрицы размерностью осуществляется методом нахождения точек оптимума функции двух переменных.

Пусть вероятность выбора игроком I первой строки платежной матрицы

равна . Тогда вероятность выбора второй строки равна .

Пусть вероятность выбора игроком II первого столбца равна . Тогда вероятность выбора второго столбца равно .

Величина платежа игроку I игроком II равна:

Экстремальная величина выигрыша игрока I и проигрыша игрока II соответствует условиям:

;

.

Таким образом, оптимальные смешанные стратегии игроков I и II соответственно равны:

5.5. Геометрическое решение игр 2× n

При увеличении размерности платежной матрицы с до уже нельзя определение оптимальных смешанных стратегий свести к нахождению оптимума функции двух переменных. Однако учитывая то, что один из игроков имеет только две стратегии, можно использовать геометрическое решение.

Основные этапы нахождения решения игры сводятся к следующему.

На плоскости введем систему координат. На оси отложим отрезок . Из левого и правого концов этого отрезка проведем перпендикуляры.

Левый и правый концы единичного отрезка соответствуют двум стратегиям и , имеющимся у игрока I. На проведенных перпендикулярах будем откладывать выигрыши этого игрока. Например, для платежной матрицы

такими выигрышами игрока I при выборе стратегии будут и , а при выборе стратегии будут и .

Соединим отрезками прямой точки выигрыша игрока I, соответствующие стратегиям игрока II. Тогда образованная ломанная линия, ограничивающая график снизу, определяет нижнюю границу выигрыша игрока I.

Находим оптимальную смешанную стратегию игрока I

,

которая соответствует точке на нижней границе выигрыша игрока I с максимальной ординатой.

Обратим внимание на то, что в рассматриваемом примере, пользуясь только двумя стратегиями и , соответствующими прямым, пересекающимся в найденной точке на нижней границе выигрыша игрока I, игрок II может воспрепятствовать игроку I получить больший выигрыш.

Таким образом, игра сводится к игре и оптимальной смешанной стратегией игрока II в рассматриваемом примере будет

,

где вероятность находится так же, как в игре :

5.6. Решение игр m × n

Если матричная игра не имеет решения в чистых стратегиях (т. е. нет седловой точки) и из-за большой размерности платежной матрицы не может быть решена графически, то для получения решения используют метод линейного программирования .

Пусть задана платежная матрица размерности :

.

Необходимо найти вероятности , с которыми игрок I должен выбирать свои ходы для того, чтобы данная смешанная стратегия гарантировала ему выигрыш не менее величины независимо от выбора ходов игроком II.

Для каждого выбранного хода игроком II выигрыш игрока I определяется зависимостями:

Разделим обе части неравенств на и введем новые обозначения:

Равенство

Примет вид:

Поскольку игрок I стремится максимизировать выигрыш , то обратную величину нужно минимизировать. Тогда задача линейного программирования для игрока I примет вид:

при ограничениях

Аналогично строится задача для игрока II как двойственная:

при ограничениях

Решая задачи симплекс-методом, получаем:

,

5.7. Особенности решения матричных игр

Прежде, чем решать задачу по отысканию оптимальных стратегий, следует проверить два условия:

Можно ли упростить платежную матрицу;

Имеет ли платежная матрица седловую точку.

Рассмотрим возможность упрощения платежной матрицы:

В связи с тем, что игрок I стремится получить наибольший выигрыш, то из платежной матрицы можно вычеркнуть - ую строку, т. к. он никогда не воспользуется этим ходом, если выполняется следующее соотношение с любой другой - ой строкой:

Аналогично, стремясь к наименьшему проигрышу, игрок II никогда не выберет в качестве хода - ый столбец в платежной матрице и этот столбец можно вычеркнуть, если выполняется следующее соотношение с любым другим - ым столбцом:

Наиболее простым решением игры является наличие в упрощенной платежной матрице седловой точки, которая отвечает следующему условию (по определению):

Пример

Дана платежная матрица:

.

Упрощение платежной матрицы:

Наличие седловой точки:

5.8. Игра с природой

В отличие от задач теории игр в задачах теории статистических решений неопределенная ситуация не имеет антагонистической конфликтной окраски и зависит от объективной действительности, которую принято называть "природой" .

В матричных играх с природой в качестве игрока II выступает совокупность неопределенных факторов, влияющих на эффективность принимаемых решений.

Матричные игры с природой отличаются от обычных матричных игр только тем, что при выборе оптимальной стратегии игроком I уже нельзя ориентироваться на то, что игрок II будет стремиться минимизировать свой проигрыш. Поэтому наряду с платежной матрицей вводится матрица рисков :

гдe - величина риска игрока I при использовании хода в условиях, равная разности между выигрышем , который игрок I получил бы, если бы знал, что установится условие , т. е. , и выигрышем , который он получит, не зная при выборе хода , что установится условие .

Таким образом, платежная матрица однозначно преобразуется в матрицу рисков, а обратное преобразование неоднозначно.

Пример

Матрица выигрышей:

.

Матрица рисков:

Возможны две постановки задачи о выборе решения в матричной игре с природой :

Максимизация выигрыша;

Минимизация риска.

Задача принятия решений может быть поставлена для одного из двух условий:

- в условиях риска , когда известна функция распределения вероятностей стратегий природы, например, случайной величины появления каждой из предполагаемых конкретных экономических ситуаций;

- в условиях неопределенности , когда такая функция распределения вероятностей неизвестна.

5.9. Решение задач теории статистических решений

в условиях риска

При принятии решений в условиях риска игроку I известны вероятности наступления состояний природы.

Тогда игроку I целесообразно выбрать ту стратегию, для которой среднее значение выигрыша, взятое по строке, максимально :

.

При решении этой задачи с матрицей риска получаем такое же решение, соответствующее минимальному среднему риску :

.

5.10. Решение задач теории статистических решений

в условиях неопределенности

При принятии решений в условиях неопределенности можно воспользоваться следующими критериями :

Максиминным критерием Вальда;

Критерием минимального риска Севиджа;

Критерием пессимизма - оптимизма Гурвица;

Принципом недостаточного основания Лапласа.

Рассмотрим максиминный критерий Вальда .

Игра с природой ведется как с разумным агрессивным противником, т. е. осуществляется перестраховочный подход с позиции крайнего пессимизма для платежной матрицы:

.

Рассмотрим критерий минимального риска Севиджа .

Аналогичный предыдущему подход с позиции крайнего пессимизма для матрицы риска:

.

Рассмотрим критерий пессимизма - оптимизма Гурвица .

Предлагается возможность не руководствоваться ни крайним пессимизмом и ни крайним оптимизмом:

где степень пессимизма ;

при - крайний оптимизм,

при - крайний пессимизм.

Рассмотрим принцип недостаточного основания Лапласа .

Полагается, что все состояния природы равновероятны:

,

.

Выводы по пятому разделу

В матричной игре участвуют два игрока и функция выигрыша, служащая для определения величины платежа проигравшего игрока выигравшему, представляется в виде платежной матрицы. Условились, что игрок I - выбирает в качестве хода одну из строк платежной матрицы, а игрок II – один из ее столбцов. Тогда на пересечении выбранных строки и столбца этой матрицы стоит числовая величина платежа игроку I от игрока II (если эта величина положительна, то игрок I действительно выиграл, а если она отрицательна, то выиграл по существу игрок II).

Если в платежной матрице имеется седловая точка, то игроки обладают оптимальными чистыми стратегиями, т. е. для выигрыша каждый из них должен повторять свой один оптимальный ход. Если же седловой точки нет, то для выигрыша каждый из них должен воспользоваться оптимальной смешанной стратегией, т. е. использовать смесь ходов, каждый из которых должен производиться с оптимальной вероятностью.

Отыскание оптимальных смешанных стратегий для игр 2×2 производится вычислением оптимальных вероятностей по известным формулам. С помощью геометрического решения игр 2×n определение оптимальных смешанных стратегий в них сводится к отысканию оптимальных смешанных стратегий для игр 2×2. Для решения игр m×n используют метод линейного программирования для нахождения оптимальных смешанных стратегий в них.

Некоторые платежные матрицы поддаются упрощению, в результате которого уменьшается их размерность за счет удаления строк и столбцов, соответствующих неперспективным ходам.

Если в качестве игрока II выступает совокупность неопределенных факторов, зависящих от объективной действительности и не имеющих антагонистической конфликтной окраски, то такую игру называют игрой с природой, а для ее решения используют задачи теории статистических решений. Тогда наряду с платежной матрицей вводится матрица рисков и возможны две постановки задачи о выборе решения в матричной игре с природой: максимизация выигрыша и минимизация риска.

Решение задач теории статистических решений в условиях риска показывает, что игроку I целесообразно выбрать ту стратегию, для которой среднее значение (математическое ожидание) выигрыша, взятое по строке платежной матрицы, максимально, или (что то же самое) среднее значение (математическое ожидание) риска, взятое по строке матрицы рисков, минимально. При принятии решений в условиях неопределенности используют следующие критерии: максиминный критерий Вальда, критерий минимального риска Севиджа, критерий пессимизма-оптимизма Гурвица, принцип недостаточного основания Лапласа.

Вопросы для самопроверки

Как определяются основные понятия теории игр: ход, стратегия и функция выигрыша?

В виде чего представляется в матричной игре функция выигрыша?

Почему матричную игру называют с нулевой суммой?

Как представляется процесс игры в матричную игру?

Какая игра называется игрой m×n?

Какая стратегия матричной игры называется оптимальной?

Какая оптимальная стратегия матричной игры называется чистой?

Что означает седловая точка платежной матрицы?

Какая оптимальная стратегия матричной игры называется смешенной?

Как представляется смешанная стратегия игрока?

Что представляет собой величина платежа игроку I от игрока II, выбравшим смешанные стратегии?

Какие смешанные стратегии называют оптимальными?

Что означает нераспределенная разность?

С помощью какого метода находятся оптимальные смешанные стратегии для игр 2×2?

Каким образом находятся оптимальные смешанные стратегии для игр 2×n?

С помощью какого метода находятся оптимальные смешанные стратегии для игр m×n?

В чем заключаются особенности решения матричных игр?

Что означает упрощение платежной матрицы и при каких условиях оно может быть осуществлено?

Какую матричную игру легче решать, когда платежная матрица имеет или не имеет седловую точку?

Какие задачи теории игр относятся к задачам теории статистических решений?

Как платежная матрица преобразуется в матрицу рисков?

Какие две постановки задачи о выборе решений возможны в матричной игре с природой?

Для каких двух условий могут быть поставлены задачи принятия решений в матричной игре с природой?

Какую стратегию целесообразно выбрать игроку I при решении задачи теории статистических решений в условиях риска?

Какими критериями принятия решений можно воспользоваться при решении задач теории статистических решений в условиях неопределенности?

Примеры решения задач

1. В платежной матрице указаны величины прибыли предприятия при реализации им разных видов изделий (столбцы) в зависимости от установившегося спроса (строки). Необходимо определить оптимальную стратегию предприятия по выпуску изделий разных видов и соответствующий максимальный (в среднем) доход от их реализации.

Обозначим заданную матрицу через и введем переменные . Будем также использовать матрицу (вектор) . Тогда и , т. е. .

Рассчитывается обратная матрица :

Находятся значения:

.

Рассчитываются вероятности:

Определяется средний доход от реализации:

.

2. Фирма «Фармацевт» - производитель медикаментов и биомедицинских изделий в регионе. Известно, что пик спроса на некоторые лекарственные препараты приходится на летний период (препараты сердечно-сосудистой группы, анальгетики), на другие – на осенний и весенний периоды (антиинфекционные, противокашлевые).

Затраты на 1 усл. ед. продукции за сентябрь-октябрь составили: по первой группе (препараты сердечно-сосудистые и анальгетики) – 20 р.; по второй группе (антиинфекционные, противокашлевые препараты) – 15 р.

По данным наблюдений за несколько последних лет службой маркетинга фирмы установлено, что она может реализовать в течение рассматриваемых двух месяцев в условиях теплой погоды 3050 усл. ед. продукции первой группы и 1100 усл. ед. продукции второй группы; в условиях холодной погоды – 1525 усл. ед. продукции первой группы и 3690 усл. ед. второй группы.

В связи с возможными изменениями погоды ставится задача – определить стратегию фирмы в выпуске продукции, обеспечивающую максимальный доход от реализации при цене продажи 40 р. за 1 усл. ед. продукции первой группы и 30 р. – второй группы.

РЕШЕНИЕ. Фирма располагает двумя стратегиями:

В этом году будет теплая погода;

Погода будет холодная.

Если фирма примет стратегию и в действительности будет теплая погода (стратегия природы ), то выпущенная продукция (3050 усл. ед. препаратов первой группы и 1100 усл. ед. второй группы) будет полностью реализована и доход составит

3050×(40-20)+1100×(30-15)=77500 р.

В условиях прохладной погоды (стратегия природы ) препараты второй группы будут проданы полностью, а первой группы только а количестве 1525 усл. ед. и часть препаратов останется нереализованной. Доход составит

1525×(40-20)+1100×(30-15)-20×()=16500 р.

Аналогично, если форма примет стратегию и в действительности будет холодная погода, то доход составит

1525×(40-20)+3690×(30-15)=85850 р.

При теплой погоде доход составит

1525×(40-20)+1100×(30-15)-() ×15=8150 р.

Рассматривая фирму и погоду в качестве двух игроков, получим платежную матрицу

,

Цена игры лежит в диапазоне

Из платежной матрицы видно, что при всех условиях доход фирмы будет не меньше 16500 р., но если погодные условия совпадут с выбранной стратегией, то доход фирмы может составить 77500 р.

Найдем решение игры.

Обозначим вероятность применения фирмой стратегии через , стратегии - через , причем . Решая игру графически методом, получим , при этом цена игры р.

Оптимальный план производства лекарственных препаратов составит

Таким образом, фирме целесообразно производить в течение сентября и октября 2379 усл. ед. препаратов первой группы и 2239,6 усл. ед. препаратов второй группы, тогда при любой погоде она получит доход не менее 46986 р.

В условиях неопределенности, если не представляется возможным фирме использовать смешанную стратегию (договоры с другими организациями), для определения оптимальной стратегии фирмы используем следующие критерии:

Критерий Вальде:

Критерий Гурвица: для определенности примем , тогда для стратегии фирмы

для стратегии

фирме целесообразно использовать стратегию .

Критерий Сэвиджа. Максимальный элемент в первом столбце – 77500, во втором столбце – 85850.

Элементы матрицы рисков находятся из выражения

,

откуда , ,

Матрица рисков имеет вид

,

целесообразно использовать стратегию или .

Следовательно, фирме целесообразно применять стратегию или .

Отметим, что каждый из рассмотренных критериев не может быть признан вполне удовлетворительным для окончательного выбора решений, однако их совместный анализ позволяет более наглядно представить последствия принятия тех или иных управленческих решений.

При известном распределении вероятностей различных состояний природы критерием принятия решения является максимум математического ожидания выигрыша.

Пусть известно для рассматриваемой задачи, что вероятности теплой и холодной погоды равны и составляют 0,5, тогда оптимальная стратегия фирмы определяется так:

Фирме целесообразно использовать стратегию или .

Задания для самостоятельной работы

1. Предприятие может выпускать три вида продукции (А, Б и В), получая при этом прибыль, зависящую от спроса. Спрос в свою очередь может принимать одно из четырех состояний (I, II, III и IV). В следующей матрице элементы характеризуют прибыль, которую получит предприятие при выпуске -ой продукции и -ом состоянии спроса:

Смешанной стратегией SA игрока А называется применение чистых стратегий A1, A2, ..., Am с вероятностями p1, p2, ..., pi, ..., pm причем сумма вероятностей равна 1: Смешанные стратегии игрока А записываются в виде матрицы или в виде строки SA = (p1, p2, ..., pi, ..., pm) Аналогично смешанные стратегии игрока В обозначаются: , или, SB = (q1, q2, ..., qi, ..., qn), где сумма вероятностей появления стратегий равна 1: Чистые стратегии можно считать частным случаем смешанных и задавать строкой, в которой 1 соответствует чистой стратегии. На основании принципа минимакса определяется оптимальное решение (или решение) игры: это пара оптимальных стратегий S*A , S*B в общем случае смешанных, обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей. Выигрыш, соответствующий оптимальному решению, называется ценой игры v. Цена игры удовлетворяет неравенству: ? ? v ? ? (3.5) где? и? - нижняя и верхняя цены игры. Справедлива следующая основная теорема теории игр - теорема Неймана. Каждая конечная игра имеет по крайней мере одно оптимальное решение, возможно, среди смешанных стратегий. Пусть S*A = (p*1, p*2, ..., p*i, ..., p*m) и S*B = (q*1, q*2, ..., q*i, ..., q*n) - пара оптимальных стратегий. Если чистая стратегия входит в оптимальную смешанную стратегию с отличной от нуля вероятностью, то она называется активной. Справедлива теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры v, если второй игрок не выходит за пределы своих активных стратегий. Эта теорема имеет большое практическое значение - она дает конкретные модели нахождения оптимальных стратегий при отсутствии седловой точки. Рассмотрим игру размера 2×2, которая является простейшим случаем конечной игры. Если такая игра имеет седловую точку, то оптимальное решение - это пара чистых стратегий, соответствующих этой точке. Игра, в которой отсутствует седловая точка, в соответствии с основной теоремой теории игр оптимальное решение существует и определяется парой смешанных стратегий S*A = (p*1, p*2) и S*B = (q*1, q*2). Для того чтобы их найти, воспользуемся теоремой об активных стратегиях. Если игрок А придерживается своей оптимальной стратегии S"A, то его средний выигрыш будет равен цене игры v, какой бы активной стратегией ни пользовался игрок В. Для игры 2×2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Выигрыш игрока А (проигрыш игрока В) - случайная величина, математическое ожидание (среднее значение) которой является ценой игры. Поэтому средний выигрыш игрока А (оптимальная стратегия) будет равен v и для 1-й, и для 2-й стратегии противника. Пусть игра задана платежной матрицей Средний выигрыш игрока А, если он использует оптимальную смешанную стратегию, а игрок В - чистую стратегию B1 (это соответствует 1-му столбцу платежной матрицы Р), равен цене игры v: a11 p*1+ a21 p*2= v. Тот же средний выигрыш получает игрок А, если 2-й игрок применяет стратегию B2, т.е. a12 p*1+ a22 p*2= v. Учитывая, что p*1+ p*2= 1, получаем систему уравнений для определения оптимальной стратегии S"A и цены игры v: (3.6) Решая эту систему, получим оптимальную стратегию (3.7) и цену игры (3.8) Применяя теорему об активных стратегиях при отыскании SВ*- оптимальной стратегии игрока В, получаем, что при любой чистой стратегии игрока А (А1 или А2) средний проигрыш игрока В равен цене игры v, т.е. (3.9) Тогда оптимальная стратегия определяется формулами: (3.10)